欧拉方法计算器
输入一阶微分方程,相关值,然后让这个计算器使用欧拉方法求解。
欧拉方法计算器
使用此欧拉方法计算器,使用欧拉方法在给定的初始条件下求解一阶微分方程。它还提供了一个分步解决方案,展示了欧拉(迭代)过程如何逼近微分方程的解,以找到解曲线上的下一个点。
什么是欧拉方法?
“欧拉方法是一种一阶数值方法,用于求解具有特定初始值的常微分方程 (ODE)”
这种方法是由瑞士数学家莱昂哈德·欧拉发明的。基本上,欧拉方法利用特定点的导数来近似函数在下一个点的值。通过使用切线,它可以估计微分方程的解。
因此,重要的是要考虑到欧拉方法是迭代方法的简化,可能无法很好地估计。因此,使用较小的步长通常会导致更精确的近似值。
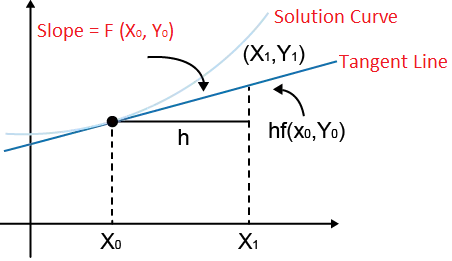
欧拉方法公式:
y (n+1) = y n + h . f(x n , y n )
在等式中:
- y n = 解上一个点的当前值
- y n + 1 = 下一步解的近似值 (n+1)
- h = 步长,控制自变量的增量
- f(x n , y n ) = 定义微分方程的函数。它表示溶液 (y) 在特定点 (x n , y n )
例:
使用步长为 1 的欧拉方法,通过以下方法近似初始值问题的 x(4) 值:
- 微分方程 = x'(t) = x(t)
- 初始条件 = x(0) = 1
解决方案(分步):
步骤#1 - 设置初始值
- 初始时间 (t 0 ) = 0
- x 的初始值 = x 0 = 1
步骤#2 - 使用欧拉方法公式
欧拉方程有不同的分量 - 获取给定的值并找到缺失的值。完成此操作后,将值放入公式中以近似于 x (4) 的解。
步骤#3 - 执行迭代
我们将重复应用 公式 四次 (n = 0, 1, 2, 3) 来近似 x(4)。为了方便用户,我们以下表的形式进行了这些计算:
|
迭代次数 (n) |
t n |
X n |
f(t , n , x n ) |
x( n + 1 ) |
|
0 |
0 |
1 |
f(0, 1) = 1 |
1 + 1 * 1 = 2 |
|
1 |
1 |
2 |
f(1, 2) = 2 |
2 + 1 * 2 = 4 |
|
2 |
2 |
4 |
f(2, 4) = 4 |
4 + 1 * 4 = 8 |
|
3 |
3 |
8 |
f(3, 8) = 8 |
8 + 1 * 8 = 16 |
步骤#4 - 解释
x(4) 的近似值为 16。它是使用 Euler 方法计算的,步长为 1 和 4 次迭代。在考虑ODE的初始值的Euler方法计算器的帮助下,可以自动执行该迭代过程。